Before immersing ourselves in the evolution of odd-n-parity functions using user defined functions, letís first analyze how UDFs work and how they are implemented in
GEP.
In gene expression programming, UDFs may represent functions of several variables although their arity in terms of expression rules is equal to zero. That is, nodes with UDFs behave as leaf nodes. So, the implementation of UDFs in GEP can be done using at least two different methods: either they are treated as terminals and are used both in the heads and tails or they are treated as functions and are used exclusively in the heads. Either way, the algorithm works very well. Thus, it is a matter of taste which one to choose. I chose the latter as it seems more consistent and less confusing. Consequently, UDFs are only used in the heads, they can occupy the first positions in the genes of the individuals of the initial population, and they can also occupy the first position of an RIS element.
Letís see now how genes containing UDFs are expressed. Consider, for instance, the chromosome below:
| 0123456789012345678 |
|
|
AON1cAA11ccacbccaba |
(4.37) |
where ď1Ē represents a UDF. Its expression results in the following ET:
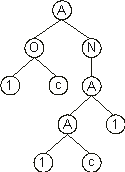
This program encodes a solution to the odd-3-parity function using XOR as
a UDF. The difference between this UDF and a normal XOR is that the arguments to the UDF are fixed during the definition of the function whereas the arguments to the XOR are flexible and depend on the particular configuration of the expression tree. For instance, in the chromosome
(4.37) above, the arguments to the UDF1 are by definition
a and b. Only now are we able to check the solution encoded in chromosome
(4.37) and confirm that, indeed, it encodes a perfect solution to the odd-3-parity function. Compare this solution with the following solution discovered using a normal XOR instead of a rigid, user defined XOR:
Nevertheless, UDFs are extremely useful, especially if they are carefully crafted to the problem at hand. As shown in
Table 4.20, the use of an inflexible XOR encapsulated in
a UDF is not much help in the evolution of solutions to the odd-5-parity and odd-6-parity functions
(Table 4.20, columns 3 and 4). However, the use of other, higher order parity functions as UDFs proves to be extremely efficient (see
Table 4.21, especially columns 3 and 4).
Table 4.20
Parameters for the odd-n-parity problem using XOR as UDF.
| |
Odd-3 |
Odd-4 |
Odd-5 |
Odd-6 |
| Number
of runs |
100 |
100 |
100 |
100 |
| Number
of generations |
50 |
50 |
100 |
300 |
| Population
size |
10 |
30 |
30 |
30 |
| Number
of fitness cases |
8 |
16 |
32 |
64 |
| Function
set |
A O N |
A O N |
A O N |
(A O
N)2 |
| User
defined functions |
X |
X |
X |
(X)2 |
| Terminal
set |
a b c |
a b c
d |
a b c
d e |
a b c
d e f |
| Head
length |
7 |
7 |
7 |
7 |
| Number
of genes |
3 |
3 |
3 |
3 |
| Linking
function |
X |
X |
X |
X |
| Chromosome
length |
45 |
45 |
45 |
45 |
| Mutation
rate |
0.044 |
0.044 |
0.044 |
0.044 |
| One-point
recombination rate |
0.3 |
0.3 |
0.3 |
0.3 |
| Two-point
recombination rate |
0.3 |
0.3 |
0.3 |
0.3 |
| Gene
recombination rate |
0.1 |
0.1 |
0.1 |
0.1 |
| Gene
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| IS
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| IS
elements length |
1,2,3 |
1,2,3 |
1,2,3 |
1,2,3 |
| RIS
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| RIS
elements length |
1,2,3 |
1,2,3 |
1,2,3 |
1,2,3 |
| Success
rate |
95% |
100% |
2% |
1% |
Table 4.21
Parameters for the odd-n-parity problem using odd-n-parity functions as
UDFs.
| |
Odd-3 |
Odd-4 |
Odd-5 |
Odd-6 |
| Number
of runs |
100 |
100 |
100 |
100 |
| Number
of generations |
50 |
50 |
100 |
200 |
| Population
size |
10 |
30 |
30 |
30 |
| Number
of fitness cases |
8 |
16 |
32 |
64 |
| Function
set |
A O N |
A O N |
A O N |
(A O
N)2 |
| User
defined functions |
Odd-2 |
Odd-3 |
Odd-4 |
Odd-5 |
| Terminal
set |
a b c |
a b c
d |
a b c
d e |
a b c
d e f |
| Head
length |
7 |
7 |
7 |
7 |
| Number
of genes |
3 |
3 |
3 |
3 |
| Linking
function |
X |
X |
X |
X |
| Chromosome
length |
45 |
45 |
45 |
45 |
| Mutation
rate |
0.044 |
0.044 |
0.044 |
0.044 |
| One-point
recombination rate |
0.3 |
0.3 |
0.3 |
0.3 |
| Two-point
recombination rate |
0.3 |
0.3 |
0.3 |
0.3 |
| Gene
recombination rate |
0.1 |
0.1 |
0.1 |
0.1 |
| Gene
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| IS
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| IS
elements length |
1,2,3 |
1,2,3 |
1,2,3 |
1,2,3 |
| RIS
transposition rate |
0.1 |
0.1 |
0.1 |
0.1 |
| RIS
elements length |
1,2,3 |
1,2,3 |
1,2,3 |
1,2,3 |
| Success
rate |
95% |
100% |
100% |
100% |
In the next section we will analyze yet another method for dealing with building blocks manipulation, namely, the use of automatically defined functions and compare it with the methods discussed before.
|
