The XOR is a simple Boolean function of two activities and, therefore, can be easily solved using linearly encoded neural networks.
The functions used to solve this problem have connectivities 2, 3, and 4, and are represented, respectively, by “D”, “T” and “Q”. For the experiment summarized in
Table 5.1, an h = 4 was chosen, allowing the discovery of hundreds of different correct solutions to the XOR function. Most of them are more complicated than the conventional solution with seven nodes shown on
section 5.1; others have the same degree of complexity evaluated in terms of total nodes; yet others are, surprisingly, more parsimonious than the mentioned conventional solution to the XOR function.
Table 5.1
Parameters for the exclusive-or problem using a redundant system (RS) and a compact system
(CS).
| |
RS |
CS |
| Number
of runs |
100 |
100 |
| Number
of generations |
50 |
50 |
| Population
size |
30 |
30 |
| Number
of fitness cases |
4 |
4 |
| Function
set |
D T Q |
D T Q |
| Terminal
set |
a b |
a b |
| Weights
array length |
10 |
10 |
| Weights
range |
[-2,
2] |
[-2,
2] |
| Head
length |
4 |
2 |
| Number
of genes |
1 |
1 |
| Chromosome
length |
33 |
17 |
| Mutation
rate |
0.061 |
0.118 |
| One-point
recombination rate |
0.7 |
0.7 |
| IS
transposition rate |
0.1 |
-- |
| IS
elements length |
1 |
-- |
| RIS
transposition rate |
0.1 |
-- |
| RIS
elements length |
1 |
-- |
| Dw
specific transposition rate |
0.1 |
0.1 |
| Dw
specific IS elements length |
2,3,5 |
2,3,5 |
| Success
rate |
77% |
30% |
The first perfect solution was found in run 0 of the experiment summarized in the first column of
Table 5.1. Its structure is shown below:
|
012345678901234567890123456789012
TQaTaaababbbabaaa6085977238275036
W = {1.175, 0.315, -0.738, 1.694, -1.215, 1.956, -0.342, 1.088, -1.694, 1.288} |
As you can see in Figure 5.4, it is a rather complicated solution to the XOR function, but remember that evolutionary algorithms thrive in slightly redundant architectures (see, e.g.,
section 7.4) and, in fact, the success rate for this problem using the less-compact chromosomal organization is higher (77%) than the obtained with more compact organizations with
h = 2 (30%).
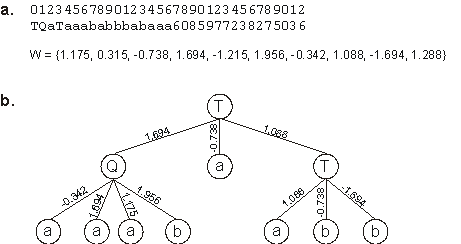
Figure 5.4. A perfect, slightly complicated solution to the exclusive-or problem evolved with GEP designed neural networks.
a) Its chromosome and respective weights. b) The fully expressed neural network encoded in the chromosome.
However, as stated earlier, GEP can be useful for searching parsimonious solutions, and a very interesting parsimonious solution to the XOR function was found in another experiment. The parameters used per run in this experiment are summarized on the second column of
Table 5.1. Note that the compact organization with
h = 2 was chosen not for its performance but rather for searching more parsimonious solutions than the conventional solution to the XOR function. One such solution is shown below:
|
01234567890123456
TDbabaabb88399837
W = {0.713, -0.774, -0.221, 0.773, -0.789, 1.792, -1.77, 0.443, -1.924, 1.161} |
which is a perfect, extremely parsimonious solution to the XOR problem. Its full expression is shown in
Figure 5.5.
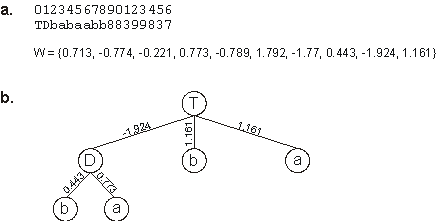
Figure 5.5. A perfect, extremely parsimonious solution to the exclusive-or problem discovered with GEP-nets.
a) Its chromosome and respective array of weights. b) The fully expressed NN encoded in the chromosome.
Curiously, in this experiment, several other solutions to the XOR function were found that use exactly the same kind of structure of this parsimonious solution. Indeed, the algorithm discovered not only one but several Boolean functions of three arguments and invented new, unexpected solutions to the XOR problem. This clearly shows that gene expression programming is an astonishing invention machine, totally devoid of preconceptions.
|

