Another way of analyzing genetic neutrality in GEP, consists of increasing the number of genes. For that purpose a compact, unigenic system capable of exactly solving the problem at hand is chosen as the starting point. Thus, the starting point for the function finding problem is a unigenic system with
h = 6 (gene length equal to 13), and h = 14 (gene length equal to 29) for the sequence induction problem (see
Figure 7.11).
As shown in Figure 7.12, the results obtained for multigenic systems further reinforce the importance of neutrality in evolution. Note that, in both experiments, the efficiency of the system increases dramatically with the introduction of a second gene and that compact unigenic systems are much less efficient than less compact, multigenic ones. For instance, in the function finding problem, the compact, unigenic system (chromosome length
c equal to 13) has a success rate of 2% whereas the success rate in the two-genic system
(c = 26) is 94%. In the sequence induction problem, the success rate in the unigenic system
(c = 29) is only 1%, whereas in the less compact two-genic system
(c = 58) it is 73%. Again, a plateau is observed where systems are most efficient, showing that a certain amount of redundancy is fundamental for evolution to occur efficiently. Indeed, it is intuitively understood that a certain room to experiment, not only by forming new building blocks but also by rejecting existing ones, is essential to come up with something new and useful. If no room is there to play, only costly (if ever) one comes up with a good solution to the problem at hand. Again, note that highly redundant systems are more efficient than extremely compact ones. For instance, the 10-genic system used in the function finding problem
(c = 130), has a success rate of 61% compared to only 2% obtained with the most compact organization
(c = 13). The same behavior can be observed in the sequence induction problem where the highly redundant 10-genic system with a chromosome length of 290 performs slightly better than the extremely compact one
(c = 29) (1% and 11%, respectively).
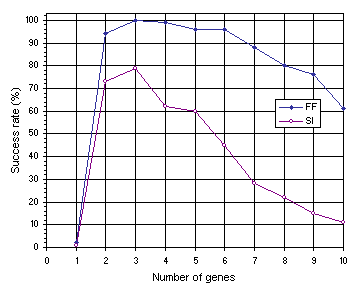
Figure 7.12. Variation of success rate with number of genes for the function finding (FF) and sequence induction (SI) problems.
The comparison of Figures 7.11 and 7.12 also shows that multigenic systems are considerably better than unigenic ones (see also
section 7.5). For instance, in the function finding problem, from two-genic to six-genic systems (corresponding to chromosome lengths 26 through 78) the success rates are in all cases above 94% and the best has a success rate of 100% (see
Figure 7.12), whereas the best chromosome length in the unigenic system
(c = 37 and h = 18) achieved only 76% (see Figure
7.11). The same phenomenon can be observed in the sequence induction problem in which from two-genic to five-genic systems (corresponding to chromosome lengths 58 through 145) the success rates are above 60% and the best has a success rate of 79% (see
Figure 7.12) whereas the best chromosome length in the unigenic system
(c = 79 and h = 39) achieved only 43% (see Figure
7.11).
The structural analysis of compact solutions and less compact ones can also provide some insights into the role of redundancy in evolution. For instance, the following perfect solutions to the sequence induction problem were obtained, respectively, for systems with one, three, and five genes:
|
(a) 01234567890123456789012345678
**a+a*a++/+/+/aaaaaaaaaaaaaaa
(b) 01234567890123456789012345678
**a+/*+a//++//aaaaaaaaaaaaaaa
/*a+/*+a//++//aaaaaaaaaaaaaaa
-*a+/-*a//++aaaaaaaaaaaaaaaaa
(c) 01234567890123456789012345678
-aa+*///-+aa/*aaaaaaaaaaaaaaa
--/*a/+/**/-/-aaaaaaaaaaaaaaa
+/-*-*a-/a+*a-aaaaaaaaaaaaaaa
aa/a/*a+*+/+/+aaaaaaaaaaaaaaa
/-/*aa++**/+/+aaaaaaaaaaaaaaa |
Note that not only the total length of the non-coding regions increases from the most compact to the less compact but also the number of neutral motifs. Specifically, the length of the non-coding region in the unigenic solution is only six and no neutral motifs are present; for the three-genic solution, the total length of the non-coding regions is 16 and three neutral motifs involving a total of 12 nodes can be counted; for the five-genic solution, the non-coding regions encompass already 66 elements and there are six neutral motifs involving a total of 31 nodes.
Because of their clarity, the results presented in this section are extremely useful for understanding the role of genetic neutrality both in artificial and natural evolution. As shown here, there are two different kinds of neutral regions in GEP: the neutral motifs within the ORFs and the non-coding regions at the end of the ORFs. In simple replicator systems such as GP or GAs, only the former exists whereas in genotype/phenotype systems such as the DNA/protein system or GEP, both kinds exist. And the presence of non-coding regions in genotype/phenotype systems is certainly entangled with the higher efficiency observed in these systems. For instance, introns in DNA are believed to be excellent targets for crossover, allowing the recombination of different building blocks without their disruption (e.g.,
Maynard Smith and Szathmáry 1995). The non-coding regions of GEP can also be used for this purpose and, indeed, whenever the crossover points are chosen within these regions, entire ORFs are exchanged. Furthermore, the non-coding regions of GEP genes are ideal places for the accumulation of neutral mutations that can be later activated and integrated into coding regions. This is an excellent source of genetic variation and certainly contributes to the increase in performance observed in redundant systems.
But, at least in GEP, the non-coding regions play another, much more fundamental role: they allow the modification of the genome by numerous high performing genetic operators. And here by “high performing” I mean genetic operators that always produce valid structures. This problem of valid structures applies only to artificial evolutionary systems for in nature there is no such thing as an invalid protein. How and why the DNA/protein system got this way is not known, but certainly there were selection pressures to get rid of imperfect genotype/phenotype mappings. The fact that the non-coding regions of GEP allow the creation of a perfect genotype/phenotype mapping, further reinforces the importance of neutrality in evolution, as a good mapping is essential for the crossing of the phenotype threshold.
On the other hand, the reason why neutral motifs within structures, be they parse trees or proteins, can boost evolution, is not so easy to understand, although I think this is another manifestation of the same phenomenon of recombining and testing smaller building blocks. In this case, the building blocks are not entire genes with clear boundaries, but smaller domains within genes. Indeed, in nature, most proteins have numerous variants in which different amino acid substitutions took place. These amino acid substitutions occur mostly outside the crucial domains of proteins such as the active sites of enzymes and, therefore, the protein variants work equally well or show slight differences in functionality. At the molecular level, these variants constitute the real genetic diversity, that is, the raw material of evolution. The neutral motifs of GEP play exactly the same function, allowing the recombination and testing of different building blocks and, at the same time, allowing the creation of neutral variants that can ultimately diverge and give birth to better adapted structures.
|
