It is known that the fruits of selection are better seen with time. Thus, we are going to analyze the performance of three different selection schemes using two different problems by evaluating the variation of success rate with evolutionary time.
The selection schemes I chose to study include the already known roulette-wheel selection used in all the problems of this book, a two-players tournament selection, and a deterministic selection scheme. For all the schemes, even deterministic selection, the cloning of the best individual is also done in order to allow the use of a fair amount of genetic modification without loosing the best trait.
The tournament selection with elitism works as follows: two individuals are randomly picked up and the best of them is chosen to reproduce once. If they happen to have the same fitness, then one of them is randomly chosen to reproduce. Thus, each generation, for populations of
N individuals, N tournaments are made so that the population size is kept unchanged.
In the deterministic selection scheme, individuals are selected proportionately to their fitnesses, but less fit individuals are excluded from the life banquet. One can choose to exclude more or less individuals from the banquet, and I have tested several deterministic selection schemes with different exclusion levels. An exclusion factor
E of 1.5 seems to be, most of the times, the best compromise.
To apply this exclusion factor, the viability (i.e., the fitness divided by average fitness) of each individual is multiplied by
E. Imagine a round table where the slices begin to be occupied by rank and proportionally to viability, starting with the best individual and finishing when no more places are available on the table. The higher the exclusion factor the more individuals die without leaving offspring and only the cream of the population reproduces. Obviously, we must be careful with the degree of exclusion, otherwise the genetic diversity is excessively reduced and evolution is seriously compromised.
The problems chosen for this study are two test problems of sequence induction. The first is the sequence
(4.9) of
section 4.2.2 and the second is the more difficult sequence
(7.1). The general settings chosen for both experiments are summarized in
Table 7.7.
Table 7.7
General settings for the sequence induction experiments used to compare different selection schemes.
| |
SI1 |
SI2 |
| Number
of runs |
100 |
100 |
| Population
size |
50 |
50 |
| Number
of fitness cases |
10 |
10 |
| Function
set |
+
- * / |
+
- * / |
| Head
length |
7 |
6 |
| Number
of genes |
5 |
7 |
| Linking
function |
+ |
+ |
| Chromosome
length |
75 |
91 |
| Mutation
rate |
0.044 |
0.044 |
| One-point
recombination rate |
0.3 |
0.3 |
| Two-point
recombination rate |
0.3 |
0.3 |
| Gene
recombination rate |
0.1 |
0.1 |
| IS
transposition rate |
0.1 |
0.1 |
| IS
elements length |
1,2,3 |
1,2,3 |
| RIS
transposition rate |
0.1 |
0.1 |
| RIS
elements length |
1,2,3 |
1,2,3 |
| Gene
transposition rate |
0.1 |
0.1 |
| Selection
range |
25% |
25% |
| Precision |
0% |
0% |
Figures 7.15 and 7.16 compare the variation of success rate obtained for the three selection schemes over a wide time span. In both experiments, the tournament selection scheme is slightly inferior to both the roulette-wheel and deterministic selection. Deciding between the roulette-wheel and deterministic selection is more problematic as for more complex problems the plots for both schemes become more intertwined
(Figure 7.16).
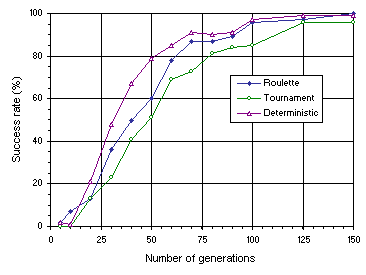
Figure 7.15. Comparison of roulette-wheel, tournament, and deterministic selection on the simpler test sequence
(4.9).
There are several reasons though why one should choose the roulette-wheel selection. (1) Real-world problems are more complex than the problems analyzed here. (2) The ideal exclusion factor depends on population size and the complexity of the problem. (3) Deterministic selection requires more CPU time as individuals must be sorted by rank and, for large populations, this is a factor to take seriously into consideration. (4) Deterministic selection is not appropriate in systems undergoing recombination alone as it reduces dramatically the genetic diversity of the population. And (5), roulette-wheel selection is easy to implement and mimics nature more faithfully and therefore is much more appealing.
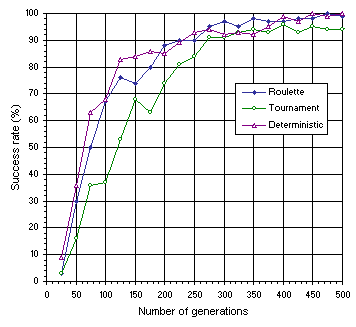
Figure 7.16. Comparison of roulette-wheel, tournament, and deterministic selection on the more difficult test sequence
(7.1).
This book finishes here and I hope to have shown you that gene expression programming is not only easy to implement but also easy to understand. Although natural evolution seems sometimes something beyond our grasp, the simple artificial system of gene expression programming can be minutely dissected in order to reveal all its secrets.
And, most of all, I hope to have convinced you that gene expression programming can help you find very good solutions to difficult real-world problems, not easily or satisfactorily solved by conventional mathematical or statistical methods.
|

