Genetic programming, invented by Cramer in 1985 (Cramer 1985)
and further developed by Koza (1992), solves the problem of fixed length solutions by creating non-linear entities with different sizes and shapes. The alphabet used to create these entities is also more varied, creating a richer, more versatile system of representation. However, GP individuals lack a simple, autonomous genome, functioning simultaneously both as genotype and phenotype. They are, therefore, simple
replicators.
The non-linear entities (parse trees) of GP resemble protein molecules in their use of a richer alphabet and in their complex and unique hierarchical representation. Thus, parse trees are capable of exhibiting a great variety of functionalities. But these entities are very difficult to reproduce because they are huge and require a lot of space. Most important, though, is that genetic modifications are done directly on the parse tree itself, restricting considerably the mechanisms of genetic modification. For instance, the simple and high-performing point mutation cannot be used as, most of the times, it generates structural impossibilities. As a comparison, it is worth emphasizing that in nature any protein gene always results in a valid protein structure.
Despite its lack of chromosomes, GP is also a genetic algorithm as it uses populations of individuals, selects them according to fitness, and introduces genetic variation using genetic operators. Thus, the fundamental difference between GP and GAs resides in the nature of the individuals and, consequently, in the way they are reproduced with modification to allow adaptation.
The individuals of genetic programming are usually LISP programs represented as parse trees
(Figure 1.8). What is particularly interesting is that parse trees may assume different sizes and shapes in the process of evolution. As such, populations may evolve and discover solutions of greater complexity.
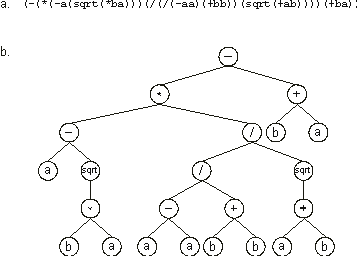
Figure 1.8. A computer program in LISP (a) and its tree representation
(b). Note that LISP operators precede their arguments, e.g.,
(a + b) is written as (+ a b).
Also worth mentioning is that, in GP, the genetic operators act directly on the parse tree and, although at first sight this might appear advantageous, it greatly limits this technique (it is impossible to make an orange tree produce mangos only by grafting and pruning). The genetic operators must be very carefully applied so that only valid structures are formed. For instance, in crossover, the most used and often only operator in GP, selected branches are exchanged between two parent trees to create offspring
(Figure 1.9). The idea behind its implementation was to exchange smaller, mathematically concise blocks in order to evolve more complex, hierarchical solutions composed of smaller building blocks. Effectively, GP crossover very much resembles the pruning and grafting of trees and, like these, has a very limited power. This kind of crossover was also devised because its implementation in LISP is trivial and the parse trees it creates are always legal LISP programs.
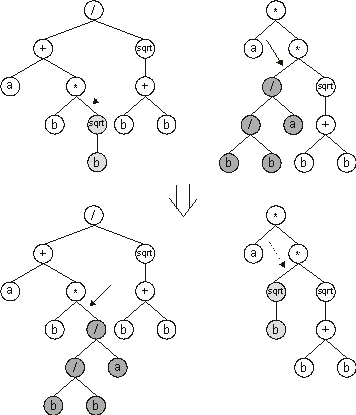
Figure 1.9. Tree crossover in genetic programming. The arrows indicate the crossover points.
The mutation operator in GP also differs from biological point mutations in order to guarantee the creation of syntactically correct LISP programs. The mutation operator selects a node in the parse tree and replaces the branch at that node by a randomly generated branch
(Figure 1.10). Again, the overall shape of the tree is not greatly changed by this kind of mutation, especially if lower nodes are preferentially chosen as mutation targets.
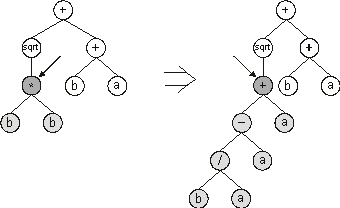
Figure 1.10. Tree mutation in genetic programming. The arrow indicates the mutation point. Note that the mutation operator creates a randomly generated branch at the mutation point.
Permutation is the third operator used in GP and the most conservative of the three. During permutation, the arguments of a randomly chosen function are randomly permuted
(Figure 1.11). In this case the overall shape of the tree remains unchanged.
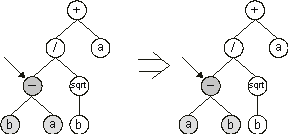
Figure 1.11. Permutation in genetic programming. The arrow indicates the point of permutation. Note that the arguments of the permuted function changed places in the daughter tree. After permutation the shape of the tree remains unchanged.
Although J. Koza described these three operators as the basic GP operators, tree-specific crossover is practically the only genetic operator used in most GP applications. Consequently, no radically new material is introduced in the genetic pool of GP populations. Not surprisingly, huge populations of parse trees must be used so that all the necessary building blocks would be already present in the initial population in order to guarantee the discovery of a good solution solely by moving the initial building blocks around.
In summary, in GP the operators resemble more of a conscious mathematician than the blind way of nature. We will see that, in adaptive systems, the blind way is much more efficient and that systems like GP are highly constrained. For instance, the implementation of other operators in GP, like the equivalent of the high-performing point mutation
(Ferreira 2002a), is unproductive as most mutations result in syntactically incorrect structures
(Figure 1.12). Obviously, the implementation of other operators such as transposition or inversion raises similar difficulties and the search space in GP remains vastly unexplored.
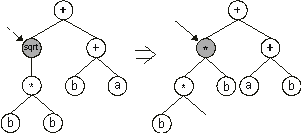
Figure 1.12. Illustration of a hypothetical event of point mutation in genetic programming. Note that the daughter tree is an invalid structure.
Finally, due to the dual function of the parse trees (genotype and phenotype), GP is incapable of a simple, rudimentary expression: in all cases, the entire parse tree is the solution.
|




