The structural organization of GEP genes is better understood in terms of open reading frames (ORFs). In biology, an ORF or coding sequence of a gene begins with the start codon, continues with the amino acid codons, and ends at a termination codon. However, a gene is more than the respective ORF, with sequences upstream of the start codon and sequences downstream of the stop codon. Although in GEP the start site is always the first position of a gene, the termination point does not always coincide with the last position of a gene. It is common for GEP genes to have non-coding regions downstream of the termination point. (For now let us not consider these non-coding regions, as they do not interfere with the product of expression.)
Consider, for example, the algebraic expression:
|
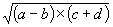
|
(2.1) |
It can also be represented as a diagram or expression tree (ET):
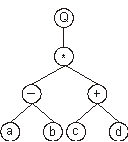
where “Q” represents the square root function.
This kind of diagram representation is in fact the phenotype of GEP chromosomes, the genotype being easily inferred from the phenotype as follows:
which is the straightforward reading of the ET from left to right and from top to bottom (exactly as we read a page of text). The expression
(2.2) is an ORF, strarting at “Q” (position 0) and terminating at “d” (position 7). I named these ORFs K-expressions (from Karva language).
Note that this notation differs from both the postfix and prefix representations used in different GP implementations with arrays or stacks
(Keith and Martin 1994). Figure 2.1 compares Karva notation both with postfix and prefix expressions.
|
K-expression:
01234567
Q*-+abcd
Postfix:
Prefix:
01234567
01234567
ab-cd+*Q
Q*+dc-ba |
Figure 2.1. Comparison of Karva notation with both postfix and prefix representations. In all cases, the expression
(2.1) is represented.
Consider another ORF, the following K-expression:
|
01234567890 |
|
|
Q*b**+baQba |
(2.3) |
Its expression as an ET is also very simple and straightforward. For its complete expression, the rules governing the spatial distribution of functions and terminals must be followed. First, the start of a gene corresponds to the root of the ET (this root, though, is at the top of the tree), forming this node the first line of the ET. Second, depending on the number of arguments of each element (functions may have a different number of arguments, whereas terminals have an arity of zero), in the next line are placed as many nodes as there are arguments to the elements in the previous line. Third, from left to right, the new nodes are filled, in the same order, with the elements of the gene. This process is repeated until a line containing only terminals is formed. So, for the K-expression
(2.3) above, the root of the ET is the symbol at position 0:
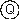
The square root function has only one argument, so the next line has only one node, which is filled with the symbol at position 1:
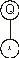
The multiplication function takes two arguments and, therefore, in the next line are placed two more nodes. These nodes are then filled with the symbols at positions 2 and 3, obtaining:
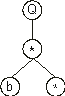
In this line we have a leaf node and a bud node representing a function of two arguments. Therefore two more nodes are required to build the next line. In this case, they are filled with the elements at positions 4 and 5, giving:
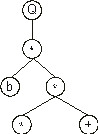
Now we have two functions in the last line, each taking two arguments. Thus, four new nodes are required in the next line. In this case, they are filled with the elements at positions 6, 7, 8, and 9, obtaining:
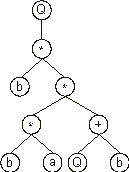
In this new line, although there are four nodes, only one of them is a bud node. In this case, the required node is placed below that function and filled with the next element in the ORF (position 10):
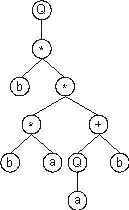
With this step, the expression of the K-expression (2.3) is complete as the last line contains only nodes with terminals. We will see that, thanks to the structural organization of GEP genes, the last line of all ETs contains exclusively terminals. This is equivalent to say that all programs evolved by GEP are syntactically correct.
Looking at the structure of the ORFs only, it is difficult or even impossible to see the advantages of such a representation, except perhaps for its simplicity and elegance. However, when ORFs are analyzed in the context of a gene, the advantages of this representation become obvious. As I said, GEP chromosomes have fixed length, and they are composed of one or more genes of equal length. Therefore the length of a gene is also fixed. Thus, in GEP, what varies is not the length of genes which is constant, but the length of the ORFs. Indeed, the length of an ORF may be equal to or less than the length of the gene. In the first case, the termination point coincides with the end of the gene, and in the latter the termination point is somewhere upstream of the end of the gene.
What is the function of these non-coding regions of GEP genes? We will see that they are the essence of GEP and evolvability, for they allow the modification of the genome using several genetic operators without restrictions, always producing syntactically correct programs. Thus, in GEP, the fundamental property of genotype/phenotype systems – syntactic closure – is intrinsic, allowing the totally unconstrained manipulation of the genotype and, consequently, an efficient evolution. Indeed, this is the paramount difference between GEP and the previous GP implementations, with or without linear genomes (for a review on GP with linear genomes see
Banzhaf et al. 1998).
Let us now analyze the structural organization of GEP genes in order to understand how they invariably code for syntactically correct programs and why they allow the unconstrained application of virtually any genetic operator.
|




