In gene transposition an entire gene works as a transposon and transposes itself to the beginning of the chromosome. In contrast to the other forms of transposition, in gene transposition, the transposon (the gene) is deleted at the place of origin. This way, the length of the chromosome is maintained.
Apparently, gene transposition is only capable of shuffling genes and, for sub-ETs linked by commutative functions, this does not contribute at all to adaptation in the short run. Note, however, that when the sub-ETs are linked by a non-commutative function, the order of the genes matters and, in this case, gene transposition is also a macromutator, generating most of the times less fitter or even nonviable individuals. However, gene transposition becomes particularly interesting when used in conjunction with recombination, for it allows not only the duplication of genes but also a more generalized recombination of genes or smaller building blocks.
Thus, for illustration purposes and because we are evolving sub-ETs linked by a commutative function, we are going to use gene transposition together with gene recombination (see
section 3.3.4.3 below). The populations shown in
Figure 3.18 are the products of nine generations of adaptation in which the only source of genetic variation was a gene transposition rate
pgt of 0.2 and a gene recombination rate pgr of 0.2. This means that the only source of novelty consisted, in this case, of moving around the genes already present in the initial population (for a comparison, the initial population is also shown in
Figure 3.18).
|
Generation N: 0
012345678900123456789001234567890
ObOaAbcabbcOcbccbbccbcAOANacccabc-[0] = 5
AbObNbbbbaaAAbaNbccbbaOANNObabcab-[1] = 4
OaaAOaaaaacOAbObcbccacNaAObaccbac-[2] = 4
AOabccbbabcAcOAbacbcbbAcNAAcababb-[3] = 7
AaAAbcbcbabOabbbbbaaccNbObNabbcbb-[4] = 4
ANAANacbabaOOcNNcbbcacOAOabaabbbb-[5] = 4
AAcaObaacaaAAbbAbaabcaNabObcbcccc-[6] = 5
AbNNccacabbNaccNbcaabaOOAaNcbabaa-[7] = 4
OcNaccabaacAacAAbbbccbANNAAbcbaac-[8] = 3
AacbbbbccaaAObbacacabcOcaabcbbcab-[9] = 5
...
Generation N: 7
012345678900123456789001234567890
AOabccbbabcAOabccbbabcANAANacbaba-[0] = 7
AacbbbbccaaAObbacacabcOcaabcbbcab-[1] = 5
AcNAAcababbAcOAbacbcbbAOabccbbabc-[2] = 7
AOabccbbabcAOabccbbabcANAANacbaba-[3] = 7
AcOAbacbcbbAOabccbbabcAcNAAcababb-[4] = 7
AacbbbbccaaAObbacacabcOcaabcbbcab-[5] = 5
AcNAAcababbOAOabaabbbbAcOAbacbcbb-[6] = 6
AcOAbacbcbbAOabccbbabcAcNAAcababb-[7] = 7
AOabccbbabcAcOAbacbcbbAcNAAcababb-[8] = 7
AacbbbbccaaAObbacacabcOcaabcbbcab-[9] = 5
Generation N: 8
012345678900123456789001234567890
AOabccbbabcAcOAbacbcbbAcNAAcababb-[0] = 7
AOabccbbabcAOabccbbabcANAANacbaba-[1] = 7
AcNAAcababbAcOAbacbcbbAOabccbbabc-[2] = 7
AOabccbbabcAOabccbbabcAcOAbacbcbb-[3] = 8
AcOAbacbcbbAOabccbbabcAcNAAcababb-[4] = 7
ANAANacbabaAOabccbbabcAOabccbbabc-[5] = 7
AcNAAcababbOAOabaabbbbANAANacbaba-[6] = 6
AOabccbbabcAcOAbacbcbbAcNAAcababb-[7] = 7
OcaabcbbcabAacbbbbccaaAObbacacabc-[8] = 5
AcOAbacbcbbAOabccbbabcAcNAAcababb-[9] = 7
|
Figure 3.18. An initial population and its later descendants created via gene transposition and gene recombination to solve the Majority
(a, b, c) function problem. The chromosomes encode
sub-ETs linked by OR. Note that the perfect solution found in generation 8 (chromosome 3) has a duplicated gene (genes 1 and 2). The ancestor genes of this individual were traced back to generation 0 and all their descendants are shown. Note how these genes got scattered throughout the genome, jumping to all conceivable places and often becoming duplicated.
It is worth noticing how genes got scattered throughout the chromosome, occupying all the positions available to them. Only gene transposition is capable of moving genes around in the chromosome. Indeed, several events of gene transposition had to occur in order to shuffle the genes so thoroughly. Such an event is illustrated below:
|
012345678900123456789001234567890
AOabccbbabcAOabccbbabcANAANacbaba-[m] = 7
ANAANacbabaAOabccbbabcAOabccbbabc-[d] = 7 |
Here, gene 3 in the mother chromosome (chromosome 3 of generation 7) moved to the beginning of the chromosome, forming chromosome 5 of generation 8 (see
Figure 3.18). Structurally, these chromosomes are different but mathematically they encode equivalent expressions. What is important is that chromosomes with the same kind of gene in different positions can recombine and might give rise to new chromosomes with duplicated genes. For instance, the perfect solution found in generation 8 (chromosome 3) has a duplicated gene. Indeed, as shown in
Figure 3.18, several chromosomes have duplicated genes (chromosomes 0 and 3 in generation 7 and chromosomes 1, 3, and 5 in generation 8). One of these chromosomes is a perfect solution to the majority function problem. Its expression is shown in
Figure 3.19.
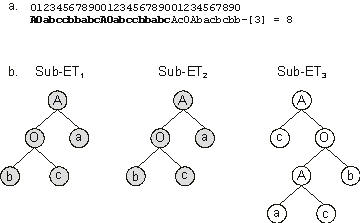
Figure 3.19. A perfect solution to the Majority (a,
b, c) function with a duplicated gene (shown in bold). These, and all duplicated genes, get duplicated only by the combined effect of gene transposition and recombination.
a) The chromosome. b) The sub-ETs encoded in the chromosome.
Although I have chosen to illustrate the combined effect of gene transposition and gene recombination with an example that also resulted in the discovery of a correct solution to the majority function, the transforming power of these operators is very limited, especially if the population sizes are very small (say, up to 500 individuals). It is worth emphasizing that these operators are unable to create new genes: they only move existing genes around and recombine them in different ways. A system creating diversity as such, could only evolve solutions to complex problems if it used gigantic populations, as all its genes would have to be present in the initial population (see
chapter 7 for a discussion).
|
