Numerical constants can be easily implemented in gene expression programming. For that an additional domain Dc is introduced in GEP genes. Structurally, the Dc comes after the tail, has a length equal to
t, and is composed of the symbols used to represent the random constants. Therefore, another region with defined boundaries and its own alphabet is created in the gene.
For each gene the constants are randomly generated at the beginning of a run, but their circulation is guaranteed by the usual genetic operators of mutation, transposition, and recombination. Besides, a special mutation operator allows the permanent introduction of variation in the set of random constants and a domain specific IS transposition guarantees a more generalized shuffling of the constants.
Consider the single-gene chromosome with an h = 7 (the Dc is shown in
blue):
|
01234567890123456789012 |
|
|
+?*+?**aaa??aaa68083295 |
(4.8) |
where the terminal ď?Ē represents the random constants. The expression of this kind of chromosome is done exactly as before, obtaining:
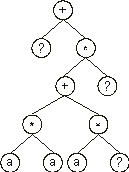
Then the ?ís in the ET are replaced from left to right and from top to bottom by the symbols (numerals) in Dc, obtaining:
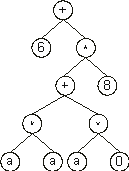
The values corresponding to these symbols are kept in an array. For simplicity, the number represented by the numeral indicates the order in the array. For instance, for the 10 elements array:
|
A = {0.611, 1.184, 2.449, 2.98, 0.496, 2.286, 0.93, 2.305, 2.737,
0.755} |
the chromosome (4.8) above gives:
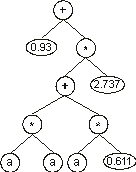
We will see later in this chapter that genes encoding this kind of domain can be used to great advantage in parameter optimization and in polynomial induction. But this elegant structure can be also used to evolve the weights and thresholds of artificial neural networks. How this is done will be explained in
chapter 5, but for now letís see how these domains of random constants can be used to do symbolic regression.
|


