The TSP represents a classical optimization problem and good, traditional approximation algorithms have been developed to tackle it down (see, e.g.,
Papadimitriou and Steiglitz 1982 for a review). However, to evolutionary computists, the TSP serves as the simplest case of a variety of combinatorial problems which are of enormous relevance to industrial scheduling problems (Bonachea et al.
2000; Hsu and Hsu 2001; Johnson and McGeoch
1997; Katayama and Narihisa
1999; Merz and Freisleben 1997;
Reinelt 1994). Indeed, several evolution-inspired algorithms used the TSP as a battleground to develop combinatorial-specific search operators (see, e.g.,
Ferreira 2002b for a detailed list of the most common combinatorial-specific operators).
For the TSP with 19 cities there are 19! = 1.21645 X 1017 combinations to search. If we fix the starting point (and consequently the ending point, for salespersons must return home), the number of possible combinations is halved to 6.0823 X
1016. Furthermore, if we choose a configuration where all the cities lie in a rectangle as shown in
Figure 6.5, we can rigorously evaluate the performance of the algorithm as we know beforehand the correct solution; for a 19 cities tour, the minimum distance will be, in this case, 20.
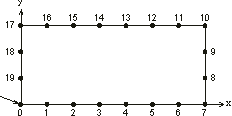
Figure 6.5. Configuration of 19 cities arranged in a rectangle. The arrow indicates the starting and finishing point. Obviously, the shortest tour is to trace the rectangle which has a distance of 20.
Obviously, we cannot use the tour length directly as a measure of fitness as the shorter the tour the fitter the individual. Thus, for each generation, the fitness
fi of an individual program i in generation
g is evaluated by the formula:
where ti is the length of the tour encoded in i, and
Tg is the length of the largest tour encoded in the chromosomes of the current population. This way, the fitness of the worst individual of the population is always equal to one. As usual, individuals are selected according to fitness by roulette-wheel selection and in each generation the best individual is cloned unchanged into the next generation. The parameters used per run are summarized in
Table 6.1.
Table 6.1
Parameters for the traveling salesperson problem with 19 cities.
| Number
of runs |
100 |
| Number
of generations |
200 |
| Population
size |
100 |
| Number
of multigene families |
1 |
| Number
of genes per multigene family |
19 |
| Chromosome
length |
19 |
| Inversion
rate |
0.25 |
| Success
rate |
96% |
The results obtained by gene expression programming are astounding if we compare them with the performance the GA achieved on the 19-city TSP. For instance,
Haupt and Haupt (1998) could not find the shortest route using population sizes of 800 for 200 generations. As shown in
Figure 6.2 and Table
6.1, the algorithm described here not only is capable of finding the shortest route using populations of only 100 individuals and for the same 200 generations, but also is capable of finding the shortest route in practically all runs (in 96% of the runs, in fact). It is worth pointing out that, in this experiment, inversion is the only source of genetic variation. Indeed, the presence of other genetic operators, namely, gene deletion/insertion and restricted permutation, decreases slightly the success rate and, therefore, these operators were not used. Apparently, they are unnecessary for finer adjustments whenever inversion is doing the search.
As stated earlier in this chapter, the chromosomal architecture used to solve combinatorial problems corresponds exactly to the canonical GA. So, why the stunning difference in performance between these two algorithms? Obviously, the answer lies in the set of genetic operators used in GEP and in GA. As shown in Figures
6.2, 6.3, and
6.4 above, inversion performs significantly better than permutation (both restricted and generalized implementations). And different kinds of permutation and extremely complicated forms of crossover (see
Ferreira 2002b for a detailed account) are exactly the kind of search operator favored by GA researchers to solve combinatorial problems. Unfortunately, inversion was abandoned earlier in the history of genetic algorithms and maybe because of this it is seldom used today even in combinatorial optimization.
|
