For this analysis, the following relatively complex test sequence was chosen:
|
an
= 5n4 +4n3 + 3n2
+ 2n +1 |
(7.1) |
where n consists of the nonnegative integers. This sequence was chosen for four reasons: (1) it can be exactly solved and therefore provide an accurate measure of performance in terms of success rate; (2) it requires relatively small populations and relatively short evolutionary times, making the task feasible; (3) it provides sufficient resolution to allow the comparison of dissimilarly performing operators such as mutation and gene recombination; and (4) it is appropriate to study all the genetic operators, including operators specific of multigenic systems like gene recombination.
In all the experiments of this section, the first 10 positive integers
n and their corresponding term an were used as fitness cases
(Table 7.1); the fitness function was evaluated by equation
(3.1b) and a selection range of 20% and maximum precision (0% error) were chosen, giving
fmax = 200; population sizes P = 500 and evolutionary times
G = 100 generations were used and the success rate Ps of each experiment was evaluated over 100 independent runs;
F = {+, -, *, /} and the terminal set consisted of the independent variable; and finally, seven-genic chromosomes of length 91 (head length
h = 6) linked by addition were used. In the experiments where transposition was switched on, three transposons with lengths 1, 2, and 3 were used.
Table 7.1
Set of fitness cases for the sequence induction problem.
| n |
an |
| 1 |
15 |
| 2 |
129 |
| 3 |
547 |
| 4 |
1593 |
| 5 |
3711 |
| 6 |
7465 |
| 7 |
13539 |
| 8 |
22737 |
| 9 |
35983 |
| 10 |
54321 |
In this section, we are going to study only six of the usual set of seven genetic operators of gene expression programming, leaving out gene transposition as, alone, this operator contributes nothing in the particular conditions chosen for this study (that is, genes encoding sub-ETs linked by addition).
The performance of all these genetic operators is shown in Figure 7.1 and, as it can be seen, mutation is the single most powerful operator, followed by RIS transposition and IS transposition, whereas recombination is the less powerful of all. Note also that the three recombinational operators show appreciable differences among themselves. As you can see, two-point recombination is the most efficient whereas gene recombination is the most inefficient. It is worth pointing out that the finger-shaped plot observed for mutation, is very different from the plots obtained both for transposition and recombination. Note that only mutation can climb “Mount Everest” and, indeed, systems undergoing mutation can be easily tuned so that populations stay, albeit precariously, poised at the peak as small variations on mutation rate have dramatic effects within the finger region.
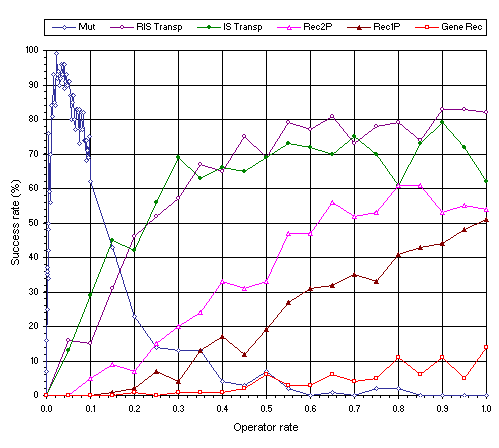
Figure 7.1. Genetic operators and their power.
As Figure 7.1 emphasizes, mutation has a tremendous creative power and, indeed, this operator alone is more than sufficient to evolve solutions to virtually all problems. Nonetheless, other genetic operators can be and are regularly used in GEP both for practical and theoretical reasons. For instance, RIS transposition is interesting as it challenges our views on the effects of too drastic modifications. Moreover, it is known that mutation is not sufficiently innovative to account for all the wonders of nature. Consider, for instance, the creation of the eukaryotes by symbiosis (Margulis
1970) or the simpler phenomenon of gene duplication (Lynch and Conery
2000) also observed in gene expression programming.
Also interesting are the results obtained for IS and RIS transposition. Particularly interesting is the fact that these two kinds of simple intrachromosomal transposition far exceed all kinds of recombination in the first place and that RIS transposition is slightly more efficient than IS transposition. It is worth pointing out that with RIS transposition the first position of a gene is always the target. And this means that, at the phenotype level, the root of sub-ETs is modified. Indeed, this kind of modification is one of the most disruptive and is similar to a frameshift mutation occurring at the beginning of a protein gene. Note also that the transforming power of both kinds of transposition is slightly smaller than mutation (compare maximum performance obtained for each operator).
Also worth discussing are the results obtained for the three kinds of recombination. Recall that two-point recombination is the most disruptive of the recombinational operators and, as shown in
Figure 7.1, it is also the most efficient kind of recombination. Not surprisingly, the most conservative of the recombinational operators – gene recombination – is also the less efficient. In addition, it is worth noticing that all the recombinational mechanisms analyzed here, even the most conservative, are more disruptive than the homologous recombination that occurs during sexual reproduction because, in GEP, the exchanged genes rarely are homologous.
One of the unsolved questions of biology is the role of sex in evolution (Margulis and Sagan
1986) and, most of the times, biological sex in its overwhelming diversity is confounded with the homologous recombination that occurs during sexual reproduction. Consequently, many erroneously assume that homologous recombination creates more diversity despite several facts against this hypothesis (Margulis and Sagan
1997). The comparison of GEP operators, especially recombination, suggests that a more conservative recombinational mechanism such as homologous recombination would only be useful for maintaining the status quo in periods of stasis. Interestingly, this hypothesis is further supported by the kind of evolutionary dynamics found in populations undergoing recombination alone (see
section 7.1.2.3).
|
